6° ÁNGULOS ENTRE RECTAS (GEOMETRÍA)

OA 16: Identificar los ángulos que se forman entre dos rectas que se cortan (pares de ángulos opuestos por el vértice y pares de ángulos Complementarios). 

OA 21: Calcular ángulos en rectas paralelas cortadas por una transversal.

Antes que todo necesitan recordar que trabajaron la clase anterior, es por eso que necesito que respondan con sus palabras las siguientes preguntas en sus cuadernos y envíen la evidencia:

1.-  Menciona todos los tipos de ángulos

2.- ¿Qué diferencia hay entre estimar y medir?

3.- Nuevamente, si te preguntan por la medida del ángulo formado en ABC. ¿la medida de que ángulo te preguntan? 

ÁNGULOS ENTRE RECTAS

A continuación analizarás distintas situaciones relacionadas con los ángulos que se forman entre rectas que se intersecan. Motívate a ser creativo y creativa al momento de desarrollar las diversas actividades.

• Dos ángulos son opuestos por el vértice si las prolongaciones de los lados de uno de ellos corresponden a los lados del otro. Estos ángulos tienen igual medida.

• Dos ángulos son complementarios si la suma de sus medidas es 90°.

• Dos ángulos son suplementarios si la suma de sus medidas es 180°.

Ejemplo 1:

Sea δ = 150°. Determina la medida de los ángulos α, β, y.

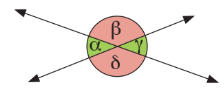
¿Cómo lo hago?

1.-  Los ángulos β y δ son opuestos por el vértice, por lo que tienen igual medida.

Luego, β = 150°.

2.-  Los ángulos α y δ son suplementarios, por lo que sus medidas suman 180°.

Luego, α = 30°.

3.-  Los ángulos α e y son opuestos por el vértice, por lo que tienen igual medida.

Luego, y = 30°.

Ejemplo 2:

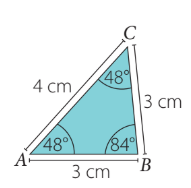
Determina el complemento y el suplemento del ángulo ABC.

¿Cómo lo hago?

1.- Calcula el complemento del ángulo ABC.

El ángulo ABC mide 55° y con su complemento deben sumar 90°.

90° – m(<ABC) = 90° – 55° = 35°

2.- Calcula el suplemento del ángulo ABC.

El ángulo ABC y su suplemento deben sumar 180°.

180° – m(<ABC) = 180° – 55° = 125°

Luego, el complemento del ángulo ABC mide 35° y su suplemento, 125°.

*Cuando dos rectas se intersecan se denominan secantes. Estas rectas pueden ser perpendiculares, si forman cuatro ángulos rectos, u oblicuas, si forman ángulos diferentes de 90°.

*Una recta transversal es aquella que se interseca con dos o más rectas.

*Si dos rectas que se prolongan indefinidamente en el plano nunca se intersecan y están siempre a la misma distancia, se denominan paralelas.

*Dos rectas son coincidentes si todos sus puntos son comunes.

TRANSVERSALES

Una recta transversal es aquella que se interseca con dos o más rectas.

Si dos rectas paralelas se intersecan con una recta transversal se forman ángulos, los

cuales cumplen con ciertas características de acuerdo a su posición y a sus medidas.

• Correspondientes: Ocupan igual posición respecto de la transversal y tienen igual medida.

• Alternos internos: Se encuentran al interior de las rectas paralelas respecto de la transversal y tienen igual medida.

• Alternos externos: Se encuentran al exterior de las rectas paralelas respecto de

la transversal y tienen igual medida.

EJEMPLO 1: 

En la siguiente imagen L1 // L2 y L3 transversal. Determina los ángulos que se forman y clasifícalos.

¿Cómo lo hago?

1.- Marca los ángulos que se forman y asígnales una letra. Luego, determina los ángulos que son correspondientes.

2.- Determina los ángulos que son alternos internos.

3.-Determina los ángulos que son alternos externos.

Ejemplo 2

Identifica los lados paralelos en el paralelogramo ABCD y determina las medidas de sus ángulos interiores.

¿Cómo lo hago?

1.-  Los lados AB y DC son paralelos y los lados AD y BC son paralelos.

2.-  Prolonga los lados del paralelogramo e identifica aquellos que sean opuestos por el vértice.

Los ángulos pintados del mismo color son opuestos por el vértice, por lo que tienen igual medida.

3.- Identifica los ángulos correspondientes y, usando los ángulos opuestos por el vértice,

determina aquellos que tienen igual medida.

 Los ángulos pintados del mismo color tienen igual medida.

4.- Determina la medida de los ángulos. Para ello identifica ángulos suplementarios.

Luego, las medidas de los ángulos interiores del paralelogramo ABCD son:

Luego de leer y escribir el contenido en tu cuaderno de geometría. Debes realizar la siguiente actividad 72 y 73 haciendo clik aquí (también debes resolver en tu cuaderno). NO OLVIDES ENVIAR LA EVIDENCIA DE TU TRABAJO CUANDO LO TERMINES.

OJO: LAS CLASES DE GEOMETRÍA SIEMPRE SERÁN PUBLICADAS LOS DÍAS JUEVES, PERO NO QUIERE DECIR QUE TODOS LOS JUEVES TENGAN NUEVO MATERIAL, YA QUE CADA MATERIAL (GEOMETRÍA) PUBLICADO SERÁ PARA 2 O 3 CLASES. 

ES POR ESO QUE EL TIEMPO ESTIMADO PARA ESTA CLASE, ES DE 2 JUEVES, IDEALMENTE EL 02 Y 09 DE ABRIL.