6° OPERACIONES, MÚLTIPLOS Y FACTORES

O.A 01: Demostrar que comprenden los factores y múltiplos: determinando los múltiplos y factores de números naturales menores de 100; identificando números primos y compuestos; resolviendo problemas que involucran múltiplos.

Antes que todo necesito que recuerdes y respondas las siguientes preguntas del contenido anterior sobre operaciones combinadas.

1) ¿Cuáles son los números naturales?

2) Menciona el orden de prioridad al resolver operatorias combinadas.

MÚLTIPLOS Y FACTORES

Un múltiplo de un número natural corresponde al producto que se obtiene al multiplicar dicho número por algún número natural.

Ejemplo
Determina los múltiplos de 5. ¿Cómo lo hago?

1) Multiplica el número 5 por algunos números naturales.

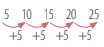
5 • 1 = 5      5 • 2 = 10     5 • 3 = 15              5 • 4 = 20     5 • 5 = 25

2) Expresa como conjunto los múltiplos pedidos.

M(5) = {5, 10, 15, 20, 25, ...}

*También puedes ir sumando el número para determinar sus múltiplos.

*El conjunto de los números naturales (N) se puede representar por: N = {1, 2, 3, ...}

Los factores de un número natural corresponden a uno o más pares de números naturales cuyo producto es igual a dicho número.

Los divisores de un número natural son aquellos números naturales que lo dividen en forma exacta.

Ejemplo

¿Cuáles son los factores y los divisores de 30? ¿Cómo lo hago?

2) Determina los factores y los divisores de 30.

Los factores de 30 son: 1 y 30; 2 y 15; 3 y 10; 5 y 6.

Observa que los factores dividen en forma exacta al número 30.

Los divisores de 30 son: 1, 2, 3, 5, 6, 10, 15 y 30.

NÚMEROS PRIMOS Y COMPUESTOS

Un número es primo si es mayor que 1 y tiene solo dos divisores, que son el número 1 y el propio número. Si tiene más de dos divisores, se dice que el número es compuesto. El número 1 no es primo ni compuesto, ya que tiene solo un divisor, que es el mismo número.

Ejemplo

Determina si el número 63 y el número 47 son números primos o compuestos, respectivamente. ¿Cómo lo hago?

1) Escribe los divisores de cada número.

Divisores de 63 --> 1, 3, 7, 9, 21 y 63            Divisores de 47 -->  1 y 47   

2) Identifica si cada número es primo o compuesto.

El número 63 es compuesto, ya que tiene más de dos divisores.

El número 47 es primo, ya que tiene solo dos divisores.

* Un número primo también lo puedes definir como aquel cuyo único par de factores es 1 y el mismo número.

Todo número compuesto lo puedes descomponer en una multiplicación de números primos. Esto se conoce como descomposición en factores primos y la puedes representar mediante un diagrama de árbol.

Ejemplo

Descompón en factores primos el número 180. ¿Cómo lo hago?

1) Representa en un diagrama de árbol la descomposición del número.

2) Escribe la descomposición del número en factores primos.

180 = 2 • 3 • 2 • 3 • 5

ALGUNOS TIPS:

• Un número es divisible por 2 si la cifra de sus unidades es par o cero.

• Un número es divisible por 3 si la suma de sus cifras es un múltiplo de 3.

• Un número es divisible por 4 si sus dos últimas cifras son ceros o forman un múltiplo de 4.

MÍNIMO COMÚN MÚLTIPLO

El mínimo común múltiplo (mcm) entre dos o más números naturales corresponde al menor de sus múltiplos comunes. Para calcularlo puedes aplicar distintas estrategias, como hacer una lista con los múltiplos o utilizar los divisores comunes de los números.

Ejemplo 1

Calcula el mínimo común múltiplo entre 6, 8 y 16. ¿Cómo lo hago?

1) Escribe una lista con los múltiplos de cada número e identifica el primero que tengan

en común.

M(6) = {6, 12, 18, 24, 30, 36, 42, 48, 54, ...}

M(8) = {8, 16, 24, 32, 40, 48, 56, 64, 72, ...}

M(16) = {16, 32, 48, 64, 80, 96, 112, 128, ...}

2) Como el menor de los múltiplos comunes entre 6, 8 y 16 es 48, entonces 

mcm(6, 8, 16) = 48.

Ejemplo 2

Calcula el mínimo común múltiplo entre 6, 8 y 16 usando otra estrategia. ¿Cómo lo hago?

1) Escribe los números en una tabla, elige un divisor común y realiza las divisiones correspondientes. Considera que los divisores deben ser números primos.

2) Continúa dividiendo cada número por sus divisores hasta que el resultado sea 1.

3) Multiplica los divisores. El producto corresponderá al mcm.

mcm(6, 8, 16) = 2 • 2 • 2 • 2 • 3 = 48.

* Cuando encuentras el primer múltiplo en común, no es necesario seguir con la lista.

Luego de haber escrito todo en el cuaderno, ponte en práctica y desarrolla desde la 10 a la 17 haciendo clik en el siguiente link.
Finalmente responde las siguientes preguntas personales con completa sinceridad:

1) ¿Qué aprendiste?

2) ¿Qué fue lo que más se te dificultó?
3) ¿Qué no lograste aprender?

No olvides enviar al correo asignado la evidencia de tú trabajo luego de haber terminado todo.